Diferenttiyhtälö, matemaattinen lause, joka sisältää yhden tai useamman johdannaisen - eli termit, jotka edustavat jatkuvasti muuttuvien määrien muutosnopeuksia. Eroyhtälöt ovat hyvin yleisiä tieteessä ja tekniikassa, samoin kuin monilla muilla kvantitatiivisen tutkimuksen aloilla, koska muutosten kohteena oleville järjestelmille voidaan suoraan havaita ja mitata niiden muutosnopeuksia. Erotusyhtälön ratkaisu on yleensä yhtälö, joka ilmaisee yhden muuttujan toiminnallisen riippuvuuden yhdestä tai useammasta toisesta; se sisältää yleensä vakiotermejä, joita ei ole alkuperäisessä differentiaaliyhtälössä. Toinen tapa sanoa tämä on, että differentiaaliyhtälön ratkaisu tuottaa funktion, jota voidaan käyttää ennustamaan alkuperäisen järjestelmän käyttäytymistä, ainakin tietyissä rajoissa.

analyysi: Newton ja differentiaaliyhtälöt
analyysin soveltaminen on differentiaaliyhtälöitä, jotka suhteuttavat eri määrien muutosnopeudet niiden nykyisiin arvoihin,
Erotusyhtälöt luokitellaan useisiin laajoihin luokkiin, ja nämä puolestaan jaetaan edelleen moniin alaluokkiin. Tärkeimmät kategoriat ovat tavalliset differentiaaliyhtälöt ja osittaiset differentiaaliyhtälöt. Kun yhtälöön liittyvä funktio riippuu vain yhdestä muuttujasta, sen johdannaiset ovat tavallisia johdannaisia ja differentiaaliyhtälö luokitellaan tavalliseksi differentiaaliyhtälöksi. Toisaalta, jos funktio riippuu useista riippumattomista muuttujista siten, että sen johdannaiset ovat osittaisjohdannaisia, differentiaaliyhtälö luokitellaan osittaisdifferenssiyhtälöksi. Seuraavat ovat esimerkkejä tavallisista differentiaaliyhtälöistä:
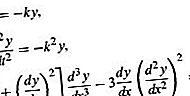
Näissä y tarkoittaa funktiota ja joko t tai x on riippumaton muuttuja. Symboleja k ja m käytetään tässä tarkoittamaan tiettyjä vakioita.
Riippumatta siitä, tyyppi voi olla, differentiaaliyhtälön sanotaan olevan n: nnen kertaluvun, jos se sisältää n: nnen asteen johdannaisen, mutta ei yhtään tätä korkeamman asteen johdannaista. Yhtälö on esimerkki toisen kertaluvun osittaisesta differentiaaliyhtälöstä. Tavallisten ja osittaisten differentiaaliyhtälöiden teoriat ovat selvästi erilaisia, ja tästä syystä kahta luokkaa käsitellään erikseen.
Yhden differentiaaliyhtälön sijasta tutkimuksen kohde voi olla tällaisten yhtälöiden samanaikainen järjestelmä. Dynamiikkalakien muotoilu johtaa usein tällaisiin järjestelmiin. Monissa tapauksissa n: nnen kertaluvun yksi differentiaaliyhtälö voidaan edullisesti korvata n samanaikaisen yhtälön järjestelmällä, joista jokainen on ensimmäisen kertaluvun yhtälö, jotta lineaarisen algebran tekniikoita voidaan soveltaa.
Tavallinen differentiaaliyhtälö, jossa esimerkiksi funktio ja riippumaton muuttuja on merkitty y: llä ja x on käytännössä implisiittinen yhteenveto y: n olennaisista ominaisuuksista x: n funktiona. Nämä ominaisuudet olisivat todennäköisesti helpommin analysoitavissa, jos y: lle voitaisiin tuottaa tarkka kaava. Tällaista kaavaa tai ainakin yhtälöä x: ssä ja y: ssä (ilman johdannaisia), joka voidaan päätellä differentiaaliyhtälöstä, kutsutaan differentiaaliyhtälön ratkaisuksi. Prosessia, jolla ratkaisua johdetaan yhtälöstä algebran ja laskennan sovelluksilla, kutsutaan yhtälön ratkaisemiseksi tai integroimiseksi. On kuitenkin huomattava, että erotteluyhtälöt, jotka voidaan selvästi ratkaista, ovat vain pieni vähemmistö. Siksi suurin osa toiminnoista on tutkittava epäsuorilla menetelmillä. Jopa sen olemassaolo on todistettava, kun sitä ei ole mahdollista tuottaa tarkastusta varten. Käytännössä käytetään numeerisen analyysin menetelmiä, joihin osallistuvat tietokoneet, hyödyllisten likimääräisten ratkaisujen saamiseksi.













