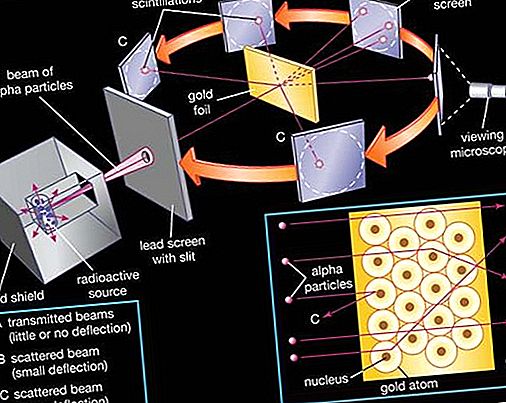
Permutaatiot ja yhdistelmät, eri tavat, joilla joukot objektit voidaan valita, yleensä ilman korvaamista, alajoukkojen muodostamiseksi. Tätä alajoukkojen valintaa kutsutaan permutaatioksi, kun valintajärjestys on tekijä, yhdistelmäksi, kun järjestys ei ole tekijä. Kun tarkasteltiin haluttujen osajoukkojen lukumäärän suhdetta kaikkien mahdollisten osajoukkojen lukumäärään monissa 1700-luvun uhkapeleissä, ranskalaiset matemaatikot Blaise Pascal ja Pierre de Fermat antoivat impulssin yhdistelmätekniikan ja todennäköisyyden teorian kehittämiselle.
yhdistelmätekniikka: Binomiaaliset kertoimet
n-esineitä kutsutaan r: n kerrallaan otettujen n-aseman permutaatioksi. Permutaatioiden lukumäärä on
Permutaatioiden ja yhdistelmien käsitteet ja erot voidaan havainnollistaa tutkimalla kaikkia erilaisia tapoja, joilla esineparia voidaan valita viidestä toisistaan erotettavissa olevasta objektista - kuten kirjaimista A, B, C, D ja E. Jos molemmat valitut kirjaimet ja valintajärjestys otetaan huomioon, seuraavat 20 tulosta ovat mahdollisia:

Jokaista näistä 20 erilaisesta mahdollisesta valinnasta kutsutaan permutaatioksi. Erityisesti niitä kutsutaan viiden objektin permutaatioiksi, jotka otetaan kaksi kerrallaan, ja tällaisten mahdollista permutaatioiden lukumäärää merkitään symbolilla 5 P 2, luetaan ”5 permute 2.” Yleensä, jos käytettävissä on n objektia, joista valita, ja permutaatiot (P) on muodostettava käyttämällä objektien k: tä kerrallaan, mahdollisten erilaisten permutaatioiden lukumäärä merkitään symbolilla n P k. Kaava sen arvioimiseksi on n P k = n! / (N - k)! Lause n! - lukee “n tekijä” - tarkoittaa, että kaikki peräkkäiset positiiviset kokonaisluvut välillä 1 - n ja mukaan lukien - on kerrottava yhdessä, ja 0! määritetään yhtä suureksi 1. Esimerkiksi tätä kaavaa käyttämällä viiden objektin permutaatioiden lukumäärä kahdessa kerrallaan on

(K = n: lle, n P k = n! Siksi viidelle esineelle on 5! = 120 järjestelyä.)
Yhdistelmille k objektia valitaan n objektin joukosta alajoukkojen tuottamiseksi ilman tilaamista. Vastoin edellistä permutaatioesimerkkiä vastaavan yhdistelmän kanssa, AB- ja BA-alajoukot eivät ole enää erillisiä valintoja; poistamalla tällaiset tapaukset, jäljellä on vain 10 erilaista mahdollista alajoukkoa - AB, AC, AD, AE, BC, BD, BE, CD, CE ja DE.
Tällaisten osajoukkojen määrää merkitään n C k, lue ”n valitse k”. Yhdistelmille, koska k esineellä on k! järjestelyt, siellä on k! erottamattomat permutaatiot jokaiselle k-kohteen valinnalle; jakamalla siten permutaatiokaava k: lla! tuottaa seuraavan yhdistelmäkaavan:
Tämä on sama kuin (n, k) binomi-kerroin (katso binomi-lause). Esimerkiksi viiden objektin yhdistelmien lukumäärä, jotka otetaan kaksi kerrallaan, on
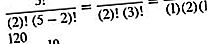
Kaavat n P k ja n- C k kutsutaan laskenta kaavat, koska niitä voidaan käyttää laskemaan Mahdollisten permutaatioiden määrä tai yhdistelmä tietyssä tilanteessa ilman luetella niitä kaikkia.