Tensoanalyysi matematiikka

Tensoanalyysi, matematiikan haara, joka liittyy suhteisiin tai lakeihin, jotka pysyvät voimassa riippumatta koordinaattien järjestelmästä, jota käytetään määrien määrittämiseen. Tällaisia ​​suhteita kutsutaan kovarianteiksi. Tenorit keksittiin vektorien jatkeena matemaattisten jakotutkimusten tutkimuksessa syntyvien geometristen kokonaisuuksien manipuloinnin virallistamiseksi.

Vektori on kokonaisuus, jolla on sekä suuruus että suunta; se on esillä nuolen piirtämällä, ja se yhdistyy samanlaisten kokonaisuuksien kanssa rinnakkaisohjelman lain mukaisesti. Tämän lain takia vektorilla on komponentteja - eri joukko jokaiselle koordinaattijärjestelmälle. Kun koordinaatistojärjestelmää vaihdetaan, vektorin komponentit muuttuvat rinnan suuntautumislakiin johdettavan muutoksen matemaattisen lain mukaan. Tällä komponenttien muutoslailla on kaksi tärkeää ominaisuutta. Ensinnäkin sen jälkeen, kun sarja muutoksia, jotka päätyvät alkuperäiseen koordinaattijärjestelmään, vektorin komponentit ovat samat kuin alussa. Toiseksi vektorien väliset suhteet - esimerkiksi kolme vektoria U, V, W siten, että 2U + 5V = 4W - ovat komponenteissa koordinaattijärjestelmästä riippumatta.

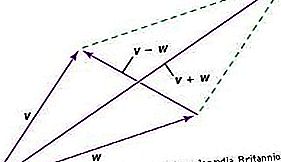
Siksi vektoria voidaan pitää kokonaisuutena, jolla n-ulotteisessa tilassa on n komponenttia, jotka muuttuvat tietyn muutoslain mukaan, jolla on yllä olevat ominaisuudet. Vektori itsessään on objektiivinen kokonaisuus, joka on riippumaton koordinaateista, mutta sitä kohdellaan komponentteina, joissa kaikki koordinaattijärjestelmät ovat tasavertaisessa asemassa.

Vaatimatta kuvaa, tensori määritellään objektiiviseksi kokonaisuudeksi, jolla on komponentteja, jotka muuttuvat muuntolain mukaan, joka on vektorimuunnoslain yleistys, mutta joka säilyttää kyseisen lain kaksi avainominaisuutta. Mukavuussyistä koordinaatit on yleensä numeroitu 1: stä n: ksi, ja jokainen tensorin komponentti on merkitty kirjaimella, jolla on ylä- ja alaindeksit, joista kukin saa itsenäisesti arvot 1 - n. Siten komponenttien T ^ab _c edustamassa ^tenorissa olisi n ³ komponenttia a: n, b: n ja c: n arvoina välillä 1 - n. Asteikot ja vektorit ovat erityisiä tapauksia tenoreista, joista ensimmäisissä on vain yksi komponentti per koordinaattijärjestelmä ja toisessa on n. Mikä tahansa tenorikomponenttien, kuten7R ^a _bcd + 2S ^a _bcd - 3T ^a _bcd = 0, välinen lineaarinen suhde, jos se on kelvollinen yhdessä koordinaattijärjestelmässä, on kelvollinen kaikissa ja edustaa siten suhdetta, joka on objektiivinen ja riippumaton koordinaatistoista huolimatta kuvallisen esityksen puute.

Kaksi tenoria, joita kutsutaan metriseksi tensoriksi ja kaarevuustestereiksi, ovat erityisen kiinnostavia. Metristä tensoria käytetään esimerkiksi muuntamaan vektorikomponentit vektorien suuruuksiksi. Yksinkertaisuuden vuoksi ota huomioon kaksiulotteinen tapaus yksinkertaisilla kohtisuorailla koordinaateilla. Olkoon vektorilla V komponentit V ₁, V ₂. Sitten oikeanpuoleiseen kolmioon OAP sovelletun Pythagoran lauseen avulla V: n suuruusaste neliö saadaan arvollaOP ² = (V ₁) ² + (V ₂) ².

Piilotettu tähän yhtälöön on metrinen tensori. Se on piilotettu, koska se koostuu 0: sta ja 1: stä, joita ei ole kirjoitettu. Jos yhtälö kirjoitetaan uudelleen muodossaOP ² = 1 (V ₁) ² + 0V ₁ V ₂ + 0V ₂ V ₁ + 1 (V ₂) ², metrisen tensorin kaikki komponentit (1, 0, 0, 1) ovat ilmeiset. Jos käytetään vinoja koordinaatteja, OP ^2: n kaava on yleisempi muotoOP ² = g ₁₁ (V ₁) ² + g ₁₂ V ₁ V ₂ + g ₂₁ V ₂ V ₁ + g ₂₂ (V ₂) ², määrät g ₁₁, g ₁₂, g ₂₁, g ₂₂ ovat metrisen tensorin uudet komponentit.

Metrisestä tensorista on mahdollista rakentaa monimutkainen tensori, jota kutsutaan kaarevuustensoriksi, joka edustaa sen n-ulotteisen tilan luontaisen kaarevuuden eri näkökohtia, johon se kuuluu.

Tenoreilla on monia sovelluksia geometriassa ja fysiikassa. Luodessaan suhteellisuusteoriaaan Albert Einstein väitti, että fysiikan lakien on oltava samat riippumatta siitä, mitä koordinaattijärjestelmää käytetään. Tämä johti hänet ilmaisemaan nämä lait tensoriyhtälöinä. Hänen erityisestä suhteellisuusteoriastaan ​​tiedettiin jo, että aika ja tila ovat niin läheisessä yhteydessä toisiinsa, että muodostavat jakamattoman nelidimensionaalisen avaruus-ajan. Einstein postuloi, että gravitaation tulisi olla edustettuna yksinomaan nelidimensionaalisen avaruus-ajan metrisen tensorin suhteen. Ilmaistakseen relativistisen painovoimalain, hänellä oli rakennuspalikoina metrinen tenori ja siitä muodostettu kaarevuustesori. Kun hän päätti rajoittua vain näihin rakennuspalikoihin, heidän heikko heikkous johti hänet olennaisesti ainutlaatuiseen gravitaatiolain tensoriyhtälöön, jossa gravitaatio ei syntynyt voimana, vaan ilmentymänä avaruus-ajan kaarevuudesta.

Vaikka tenoreita oli tutkittu aiemmin, Einsteinin yleisen suhteellisuusteorian menestys johti siihen, että matemaatikot ja fyysikot ovat nykyään laajalti kiinnostuneita tenoreista ja heidän sovelluksistaan.